By :?yudan@慢雾安全团队
By:? yudan@ slow fog security team
目前,使用 LP Token 进行抵押借贷的需求越来越大,但是目前市面上并没有一种完善的用于安全获取 LP Token 价格的方法。慢雾安全团队在分析 LP Token 价格的获取方式的过程中关注到了 Alpha Finance 团队的关于安全获取 LP 价格的方法。在仔细阅读后,将相关的思考分享给大家。
Currently, there is an increasing demand for mortgage lending using LP Token, but there is currently no perfect method on the market to secure LP Token prices. The slow fog security team has focused on the Alpha Finance team's approach to secure LP prices in its analysis of how LP Token prices are obtained.
目前,常见的 LP Token 价格的获取方式如下:
Currently, the usual LP Token prices are obtained as follows:
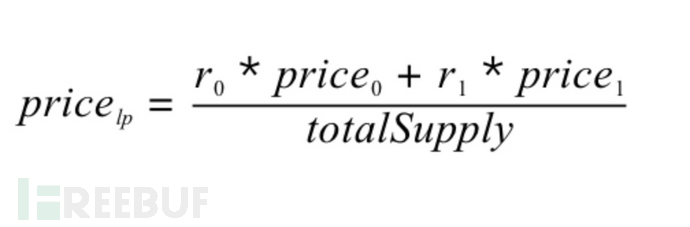
其中,r0,r1 分别代表 Uniswap 交易对中两种代币的存量,price0,price1 分别代表 r0 和 r1 对应代币的价格。上面的公式简单来说就是算出交易对中两种代币的总价值之和,然后除以 LP Token 的总数量,得到了单份 LP 的价值。
Of these, r0, r1 represents, respectively, the stock of Uniswap transactions for the two currencies, and the price of r0 and r1 for each of them. The formula is simply to calculate the sum of the total value of the transaction for the two currencies and then to divide it by the total quantity of LP Token and get a single share of the LP value.
这个公式咋一看没什么问题,一般来说,price0 和 price1 都会取 Uniswap 本身提供的延时价格。但是这里存在一个被闪电贷攻击的风险。虽然 price0 和 price1 是不能操控的,但是 r0 和 r1 却是可以操控的。通过操控 r0 和 r1 的值,即可对整个公式进行操控,具体可参考慢雾文章《采用延时喂价还被黑?Warp Finance 被黑详解》
The value of r0 and r1 is easy to manipulate the entire formula by reference to slow-mortage articles 那么有没有办法能获取一种安全的 LP Token 价格,使代币的存量无法被操控呢?Alpha Finance 团队提供了一个思路: So is there any way to get a safe LP Token price that doesn't allow the stock of the tokens to be manipulated? The Alpha Finance team provides a thought: 根据 Alpha Finance 的分析,整个过程分为 3 步: According to Alpha Finance analysis, the process was divided into three steps: 第 1 步是通过 Uniswap 的 getReserves 接口获得交易对中对应代币的数量,算出 K Step 1 gets the number of coins to be traded through the getReserves interface of Uniswap and calculates K 第 2 步是获取交易对中每个代币对应的价格,然后算出代币的价格的比例 P Step 2 is to capture the price of the transaction in relation to each of the currencies and then calculate the price of the currency P 第 3 步是通过 K 和 P 之间的关系反推真实的代币存量。 Step 3 reverses the real currency stock through the relationship between K and P. 完成以上 3 步后,最终 LP Token 的价格获取公式会变成下面这个样子: After completing the above three steps, the LP Token price acquisition formula eventually becomes the following: 这一波操作下来,好像有点整懵了,但是问题不大,我们来逐个分析。 The wave came down a little rough, but it's not a big problem, so let's look at it one by one. 首先,我们知道,Uniswap 采用的是恒定乘积算法。简单来说就是?x * y=K,也就是说,交易前后的 K 值是不会变的。在不讨论手续费的情况下,K 值理论上是不会改变的。我们先记住这个前提。然后,获取交易对中每个代币各自的价格,比方说对 USDT 价格。这里以 ETH-BTC 交易对为例,假设 ETH 的价格为 650 USDT,BTC 的价格为 22,000 USDT,那么 ETH/BTC 的价格比值 P 为 0.03。在得到价格的比值 P 之后,直接用第 1 步得到的 K 计算 K/P 和 K*P 就得到了对应交易对的一个正常的数量。下面要对第 3 步,即获取正常的数量这一步进行相应的说明。 First, we know that Uniswap uses constant multiplier algorithms. Simplely speaking, 现在开始对上面的第 3 步进行说明,扶稳坐好 :D Let's start with step 3 above. Hold tight: D. 像前面说的,恒定乘积的公式为: As stated earlier, the formula for constant multiplying is as follows: 那么其实可以根据 K 来分别算出 x,y。然后根据上一节的第 2 步,我们得到了 x 和 y 的价格的比值 P。由于 Uniswap 本身是根据池中代币的比例来确定对应的价格,所以比值 P 本身就是 x/y 的价格的比值。然后,由于?K=x * y,而 P 是由正确的价格算出的比值,那么,我们其实就可以以这个真实的 K 和 x/y 来反推真实的 x 和 y 。 Then the value of x, y, can be calculated separately from K. Then, according to step 2 of the previous section, we get the price ratio of x and y P. Since Uniswap itself determines the price by the ratio of the coins in the pool, the value P is the price ratio of x/y itself. Then, because K=x/ strong>, and P is the ratio of the correct price, we can actually invert the real x and y with this real K and x/ y. 推算如下: The calculations are as follows: 首先,我们根据 P 和 r0,r1 的比例得出以下公式: First, we arrive at the following formula based on the P and r0, r1 ratio: 接着,根据 P 就可以倒推真实的 r0,r1,如下: Then, according to P, the real r0 r1, as follows: 那么,拿到了正确比例的 x 和 y 之后,LP 的价格会是下面这个公式: So, when you get the right ratio of x and y, the price of the LP will be the following formula: 再转换成如下: and replace it with the following: 在完成公式分析后,我们不难知道,只要有正确的价格的比例 P,就能根据这个比例倒推真实的 r0 和 r1,最后得到公式: After completing the formula analysis, it is easy to know that if there is a ratio of the right price P, we can push the real r0 and r1, based on this ratio, and finally get the formula: 那么,这个公式能不能被攻击呢?从公式上可以知道,公式的 price0,price1 都是可信源获取的正确的价格,这个值是无法被操控的,然后是 totalSupply,这个值虽然可以操控,但是在控制 LP 价格进行攻击的过程中改变 totalSupply 只能是改变你的抵押数量,这个暂时没有用。那么剩下可以操控的只有 r0 和 r1 的值了。如何改变 r0,r1 的值呢?下面提供两种思路进行分析: So, can this formula be attacked? From the formula, it is known that the formula's price 0, price 1 is the correct price that can be obtained from a credible source. This value can't be manipulated, and then totalSupply, which changes totalSupply in the course of controlling the LP price attack, but only totalSupply can change your collateral, which is temporarily useless. Then only r0 and r1 values can be manipulated. How can the values of r0, r1 be changed? 我们知道,在代币池中,无论是采用什么算法进行计算,代币池在进行代币兑换的过程中,必然会发生代币数量的改变,那么这种改变最终能不能操控公式呢?其实是不可以的。我们知道,在恒定乘积的模型中,x * y=K总是成立的,那么也就是说无论交易过程中怎么发生代币的兑换,K 的值总是不变的(这里不考虑手续费的情况),而公式中采用的是 r0 和 r1 进行相乘,所以使用代币兑换来操控公式实际上是不可行的。 We know that in the currency pool, regardless of the algorithm used to calculate it, there will always be a change in the number of coins during the process of currency exchange, so can this change eventually manipulate the formula? It is not possible. We know that in the constant multiplier model, x*y=K is always established, so that regardless of how the exchange of coins takes place in the course of the transaction, K's value is always constant (where no transaction costs are taken into account), whereas R0 and r1 are used in the formula, so it is practically not feasible to use a proxy exchange to manipulate the formula. 这种思路比较粗暴,可以直接忽视 K 值来操控 r0 和 r1 相乘的值,但是经过我的运算,这种方法看似可行,其实是不行的。虽然达到了操控的目的,但是因为公式本身在获取最终价格的时候采用的是根号的模式,所以最后获得的收益是根号后的收益,比方说付出 10,000 的成本,最后只能获得最多 100 的收益,这样是明显不划算的。所以这种思路也是不可行的。 This approach is rough enough to ignore the K value to manipulate R0 and R1, but, by my calculations, it seems to be workable and not possible. Although the purpose of manipulation has been achieved, because the formula itself uses a root number model when it comes to obtaining the final price, the final gain is the profit after the root, for example, by paying 10,000, with a maximum of 100, which is clearly not cost-effective. 本算法的适用范围仅限于适用 AMM 模型的代币池的 LP 价格的获取,因为整个推导过程都基于恒定乘积公式中 K 的基本特性来进行。获取的 LP 本身所属的交易对算法不使用 AMM 模型是不可行的,因为这种情况下,前面所有的假设都已经不成立了,那么对应的公式的推算自然也是不成立的。 The scope of application of this algorithm is limited to the acquisition of the LP price for the currency pool to which the AMM model applies, because the entire process of deduction is based on the basic properties of K in the constant multiplier formula. The acquisition of the LP itself is not feasible for the algorithm without the AMM model, because in this case all previous assumptions are no longer established, and the calculation of the corresponding formula is naturally invalid. LP 抵押已经成为了一种迫切的需求,在目前没有更好的方式(如 ChainLink 提供的 LP 喂价,Uniswap 提供延时 LP 接口等),Alpha Finance 的方式可以说是一种较为安全的实现方法,使针对数量进行控制的攻击变成不可行或成本非常高。当然,随着越来越多场景的出现,这种算法也不一定是万能的,项目方需要结合自身的场景,合理运用该算法,达到良好的效果。此外,特别需要注意的是,虽然公式的终极形式用的是开根号的 r0,r1 和 price0,price1 相乘,但是真正实现的时候,需要根据 K 来推导具体的 r0 和 r1 的值,不然会存在一定的误差。 LP mortgages have become an urgent need, and there is no better way at present (such as the LP feed price provided by ChainLink, Uniswap provides a delayed LP interface, etc.), Alpha Finance is a safer way to achieve, making a controlled attack on numbers unworkable or very costly. Of course, as more and more scenes emerge, the algorithm is not necessarily all-powerful, and the 参考链接:Alpha Finance 关于获取公平? LP 价格的方法 Reference link: Alpha Finance on Access to Equity? 

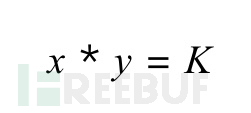
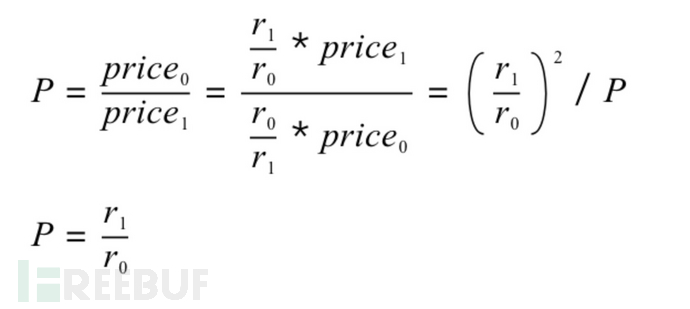
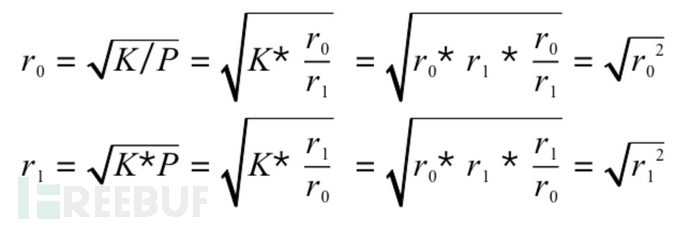
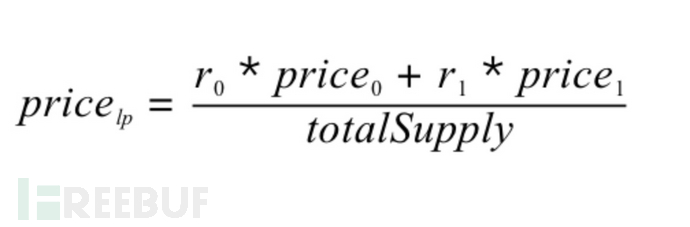
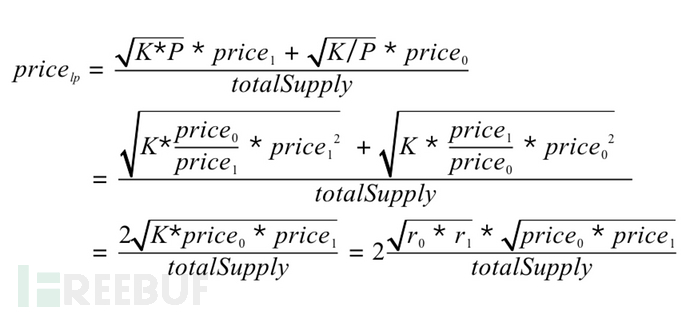
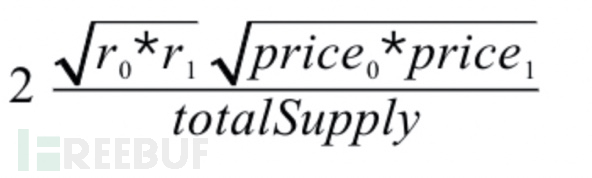
注册有任何问题请添加 微信:MVIP619 拉你进入群

打开微信扫一扫
添加客服
进入交流群


















发表评论